Esses sistemas de equações podem ser resolvidos de quatro formas diferentes: método de substituição, método de adição, método de comparação e método gráfico.
Não se assuste! Você não precisa ser um especialista em todos os métodos de resolução. Entretanto, considere que o sabre aplicar corretamente pelo menos dois métodos vai ajudar bastante.
Quais são os melhores métodos?
Não existe o melhor método de resolução do ponto de vista geral.
Para cada sistema de equações existe um método de resolução que se encaixa melhor, que facilitará sua vida e que fará você perder menos tempo e energia.
Dentro de um contexto de concurso público, ganhar tempo e não se desgastar numa questão de prova são virtudes que levarão você ao seu objetivo: aprovação no concurso público pleiteado.
1º) Resolução pelo método da substituição
Voltando aos métodos de resolução dos sistemas de equações com duas incógnitas, vamos iniciar com o método da substituição. Usaremos o sistema de equações do 1º grau com duas incógnitas abaixo.
\(left{begin{matrix} 3x+2y=12 \ x-3y=-7 end{matrix}right.\)O método da substituição possui quatro etapas bem definidas.
Solução
1ª) Determinar o valor de x, em função de y, na segunda equação.
Fizemos essa escolha porque a incógnita x, na segunda equação, possui coeficiente igual a 1. Essa escolha facilita o isolamento da incógnita x em relação aos outros termos da equação.
\(large \ x-3y=-7\ x=-7+3y\)2ª) Substituímos o valor de x, em função de y, na primeira equação.
\(large \ 3x+2y=12\ 3(-7+3y)+2y=12\)3ª) Resolvemos a equação formada apenas com a incógnita y.
\(\3(-7+3y)+2y=12\ \-21+9y+2y=12\ \9y+2y=12+21\ \11y=33\ \y=frac{33}{11}\\ y=3\)Dessa forma, encontramos o valor de \(y.\)
4ª) Substituímos, em qualquer das equações, o valor encontrado para \(y\), para determinar \(x\).
Aplicando \(y=3\) na segunda equação, obtemos:
\(large \x-3y=-7\ \x-3(3)=-7\ \x-9= -7\ \x= -7 + 9\ \x= 2\)Atente-se que \(U= R X R\), isso indica que os possíveis valores para \(large x\) e \(large y\) devem pertencer ao conjunto dos números reais. Caso contrário, o sistema é impossível, ou seja, não tem solução no conjunto universo proposto \((R X R)\).Em fim, determinamos os valores para as duas incógnitas, logo a solução do sistema é o par ordenado \((2,3)\), ou seja, \(V={(2,3)}\).O vídeo abaixo apresenta todo o processo dinâmico dessa resolução.
O vídeo abaixo apresenta todo o processo dinâmico dessa resolução.
Você percebeu que o método da substituição possui um passo-a-passo organizado e ágil?
Quanto mais sistemas de equações do 1º grau com duas incógnitas você resolver utilizando o método da substituição, mais você se torna um especialista nesse método.
Aqui vai uma dica de metodologia de estudo: comece pelos sistemas mais simples e, aos poucos, aumente o grau de dificuldade desses sistemas até chegar aos mais complexos.
2º) Resolução pelo método da adição
Ao contrário do método da substituição, o método da adição será aplicado quando tivermos – para uma determinada incógnita – coeficientes opostos nas duas equações.
Nem sempre você terá a sua frente um sistema de equações que possui coeficientes opostos nas duas equações do sistema.
A seguir apresentamos um sistema de equações onde a aplicação do método da adição é direta e imediata.
\(left{begin{matrix} x+2y=5 \ 3x-2y=-25 end{matrix}right.\)Veja que a incógnita \(large y\) tem coeficientes opostos \((-2,+2)\) nas duas equações, por isso pode ser eliminada.
Nesse caso, o método da adição possui duas etapas de resolução.
Solução
1ª) Adicionamos membro a membro as equações.
\(left{begin{matrix} x+2y=5 \ 3x-2y=-25 end{matrix}right.\)\(large \ 4x+0=-20\ 4x= -20 \\ x= frac{-20}{4}\\ x= – 5\)
2ª) Substituímos, em qualquer das equações, o valor encontrado de \(large x\), para determinar \(large y\).Aplicando \(large x=-5\) na primeira equação, obtemos:
\(\x+2y=5\ \-5+2y=5\ \2y=5+5\ \2y=10\ \y= frac{10}{2} \ \y=5\)A solução do sistema é o par ordenado \((-5,+5)\), então \(V=left {x in R e y in Rsetminus x=-5 e y=+5 right }\).
O método da adição é ágil quando temos coeficientes opostos nas equações.
Você lembra que eu disse que nem sempre teremos coeficientes opostos nas duas equações?
Então, podemos resolver pelo método da adição também. Você terá apenas que preparar esse sistema de modo que você tenha coeficientes opostos para uma determinada incógnita nas duas equações.
A seguir apresentamos um sistema de equações onde a aplicação do método da adição não é direta.
\(left{begin{matrix} 2x + 3y = 14 \ x-5y=-6 end{matrix}right.\)Veja que tanto a incógnita \(x\), quanto a incógnita \(x\) não possuem coeficientes opostos nas duas equações. Essa segunda forma de utilizar o método da adição possui quatro etapas.
Solução
1ª) Multiplicamos a segunda equação por \(-2\), para que o coeficiente da incógnita \(x\) fique com o valor oposto ao coeficiente da primeira equação.\(large \-2(x-5y)= -2(-6)\\ -2x+10y= +12\)
Acabamos de obter uma equação equivalente à segunda equação do sistema. Vamos usá-la.
\(left{begin{matrix} +2x + 3y = 14 \ -2x+10y=12 end{matrix}right.\)3ª) Adicionamos membro a membro as duas equações.
\(left{begin{matrix} +2x + 3y = 14 \ -2x+10y=12 end{matrix}right.\)\(large \0+13y=26\ \13y=26\ \y=frac{26}{13}\ \ y=2\)4ª)Substituímos, em qualquer das equações, o valor encontrado de \(y\), para determinar \(y\).Aplicando \(y=2\) na primeira equação do sistema inicial, obtemos:\(\2x+3y=14\ \2x+3(2)=14\ \2x+6=14\ \2x=14-6\ \2x=8\ \x=frac{8}{2}\)A solução do sistema é o par ordenado \((4,2)\), então \(V=left { xin R e yin Rsetminus x=4 e y=2 right }\).Veja a seguir o vídeo contendo as duas resoluções pelo método da adição.
Você percebeu que o método da adição pode ser usado em praticamente todas as situações?
Claro, será muito mais fácil quando o sistema tiver coeficientes opostos para uma das incógnitas do sistema.
Particularmente, quando o momento exige rapidez da minha parte, utilizo o método da adição apenas quando o sistema possui coeficientes opostos nas duas equações do sistema.
Crie sua própria estratégia, trace a sua história!
3º) Resolução pelo método da comparação
Lembre-se de que quanto mais você pratica cada um dos métodos, mais você ganha experiência e evolui no conteúdo.
O método da comparação restringe-se em isolar a mesma incógnita nas duas equações do sistema, comparando as igualdades.
Usaremos o sistema de equações abaixo para aplicarmos o método da comparação.
\(left{begin{matrix} x-2y=-7 \ 3x+y=0 end{matrix}right.\)Solução
1ª) Isolamos a incógnita \(x\) na primeira equação.
\(large \x-2y= -7\ \x= -7+2y\)2ª) Isolamos a incógnita x na segunda equação.
\(large \3x+y=0\ \3x= -y\ \x=frac{-1y}{3}\)3ª) Comparamos as igualdades obtidas.
\(\-7+2y=frac{-1y}{3}\ \frac{-21+6y}{3}=frac{-1y}{3}\ \-21+6y= -1y\ \6y+1y=21\ 7y=21\ y=frac{21}{7}\ y=3\)
4ª) Substituímos, em qualquer das equações, o valor encontrado para \(y\) para determinar \(x\).
Aplicando \(y=3\) na primeira equação, obtemos:\(large \x-2y= -7\ x-2(3)= – 7\ x-6= -7\ x= -7+6\ x= -1\\)
A solução do sistema é o par ordenado \((-1,+3)\), então \(V=left { (-1,+3) right }\).
Caso queira, você pode acompanhar essa resolução em vídeo onde eu coloco a mão na massa e mostro na sequência cada detalhe dessa resolução.
4º) Resolução pelo método gráfico
O método gráfico é o método menos usual, mas não o despreze com muita facilidade. Algumas questões de concurso cobram esse tipo de resolução.
Usaremos o sistema de equações abaixo para aplicar o método gráfico.
\(left{begin{matrix}2x+y=-4 \ x+3y=-2 end{matrix}right.\)Solução
Cada equação do nosso sistema representa uma reta no plano cartesiano. Dessa forma, nós representaremos essas duas retas no plano cartesiano.
A reta p está associada à equação \(2x+y= -4\).
A reta q está associada à equação \(x+3y= -2\).
1ª) Encontrar dois pontos da reta p para posteriormente traçar a reta p no plano cartesiano.
Para traçar esse reta, basta encontrarmos dois pontos dessa reta.
Basta fazer \(x=0\) e descobrir o valor de \(y\).
Dessa forma, temos o primeiro par ordenado.
\(large \2x+y= -4\ 2(0)+y= -4\ y= -4\)O primeiro par ordenado é \((0,-4)\).
Em seguida, façamos \(y=0\) e descobriremos o valor de \(x\).
\(large \2x+y= -4 \2x+0= -4 \2x= -4 \x=-42 \x=-2\)O segundo par ordenado é \((-2,0)\).
2ª)Encontrar dois pontos da reta q para posteriormente traçar a reta q no plano cartesiano.
Façamos \(x=0\) para o primeiro ponto.
\(large \x+3y= -2\ \0+3y= -2\ \y=frac{-2}{3}\)O primeiro ponto é \((0, -23)\).
Façamos \(y=0\) para o segundo ponto.
\(large \x+3y= -2\ \x+3(0)= -2\ \x= -2\)O segundo ponto é \((-2,0)\).
3ª) Traçar duas retas no plano cartesiano.
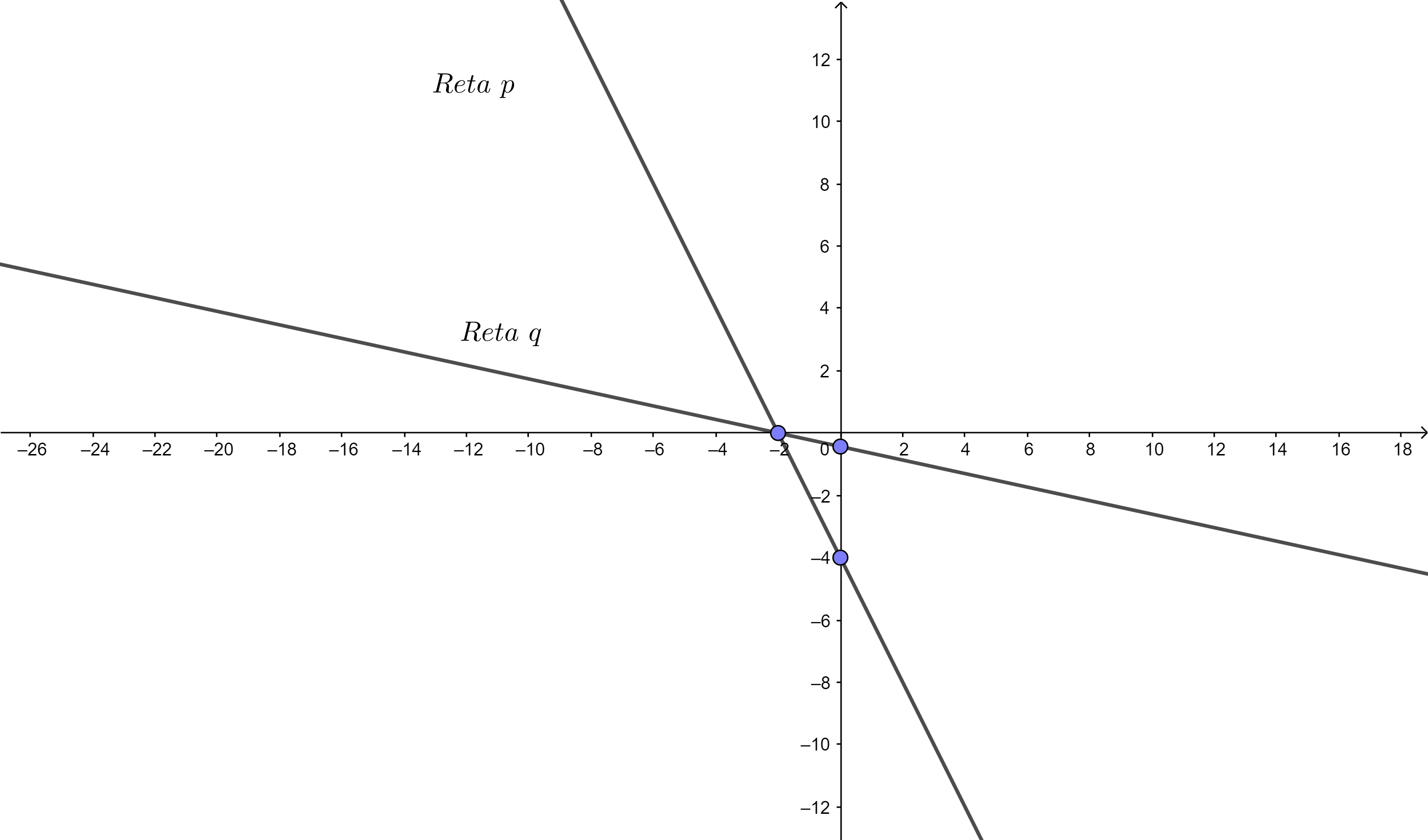
Como as retas p e q são concorrentes (ou seja, se cruzam em apenas um ponto), dizemos que o sistema é determinado.
A solução fica representada pelo par ordenado do ponto de intersecção das duas retas.
O ponto \((-2,0)\), intersecção das retas p e q, é a solução do sistema.
Portanto, \(V=left { (-2,0) right }\).
Conforme falei anteriormente, o método gráfico é pouco utilizado. Sugiro utilizá-lo apenas nas questões que exigir esse tipo de resolução.
Nem sempre as retas serão concorrentes e, consequentemente, teremos uma única solução.
Além dessa, há duas possibilidades ainda:
- As retas são paralelas e não haverá nenhum ponto em comum. Nesse caso, o sistema é impossível.
- As retas são coincidentes, ou seja, teremos infinitos pontos em comum. Nesse caso, o sistema é indeterminado.
Vamos agora acompanhar essa resolução em vídeo.
Nesse momento, você passou a conhecer melhor todos os métodos de resolução dos sistemas de equações do 1º grau. Certamente você deve ter se familiarizado com um dos métodos.
Lembre-se: não há necessidade de utilizar todos os métodos de resolução. Saiba aplicar muito bem pelo menos um deles e isso já terá grande valor.
Aguardo você nos próximos artigos!



