Aprenda a negar as proposições que contenham os quantificadores Todo, Algum e Nenhum

A cobrança dos quantificadores todo, algum e nenhum nas provas de concursos públicos é altamente recorrente.

Nesse artigo falaremos da negação desses quantificadores de modo que você possa assimilar o conteúdo da melhor forma possível.

Mas o que significa na prática negar uma proposição?

Rápido e direto, negar uma proposição lógica significa trocar o seu valor lógico. Vamos ao exemplo.

Considere as proposições simples p e q abaixo.

p: Marcelo gosta de ler romance.

q: João não é motorista de aplicativo.

Faremos a negação das proposições p e q.

~p: Marcelo não gosta de ler romance.

~q: João é motorista de aplicativo.

Vamos considerar que o valor lógico de p seja verdade e o valor lógico de q seja falso.

V(p) = V

V(q) = F

Veja que, quando fizemos a negação das proposições p e q, mudamos o valor lógico dessas proposições.

V(~p) = F

V(~q) = V

Dessa forma, negar uma proposição lógica implica trocar o seu valor lógico. De forma mais objetiva, a negação de uma proposição verdadeira é uma proposição falsa e a negação de uma proposição falsa é uma proposição verdadeira.

Portanto, já sabemos o que acontece com o valor lógico de uma proposição quando fazemos a negação dessa proposição. Grosso modo, ela troca o seu valor lógico.

Agora, o que podemos falar sobre os quantificadores?

No dicionário, podemos afirmar que quantificador indica palavra que exprime quantidade, por exemplo, todo, muito, pouco, cada.

Em outras palavras, quantificadores são palavras ou expressões que indicam que houve quantificação.

Seguem outros exemplos de quantificadores: existe, algum, todo, cada, pelo menos um, nenhum.

Os quantificadores podem ser classificados em dois tipos: quantificador universal e quantificador existencial.

Conectando tudo isso com as proposições lógicas, podemos declarar dois tipos de proposições: as proposições universais e as proposições existenciais.

Vamos a alguns exemplos:

TIPOS DE PROPOSIÇÕES	EXEMPLOS
Proposição Universal	Todo goiano é brasileiro.
Proposição Existencial	Algum goiano é brasileiro.

Além dessas classificações apresentadas: proposição universal e proposição existencial, podemos dizer se essas proposições são afirmativas ou negativas.

Vamos apresentar mais alguns exemplos, só que agora combinando essas classificações.

TIPOS DE PROPOSIÇÕES	EXEMPLOS
Proposição Universal Afirmativa	Todo goiano é brasileiro.
Proposição Universal Negativa	Nenhum goiano é brasileiro.
Proposição Existencial Afirmativa	Algum goiano é brasileiro.
Proposição Existencial Negativa	Algum goiano não é brasileiro.

Para fazer a negação das proposições que contém os quantificadores todo, algum e nenhum, você precisa saber classificar essas proposições.

A classificação var depender do tipo do quantificador.

O esquema abaixo indica as possíveis situações.

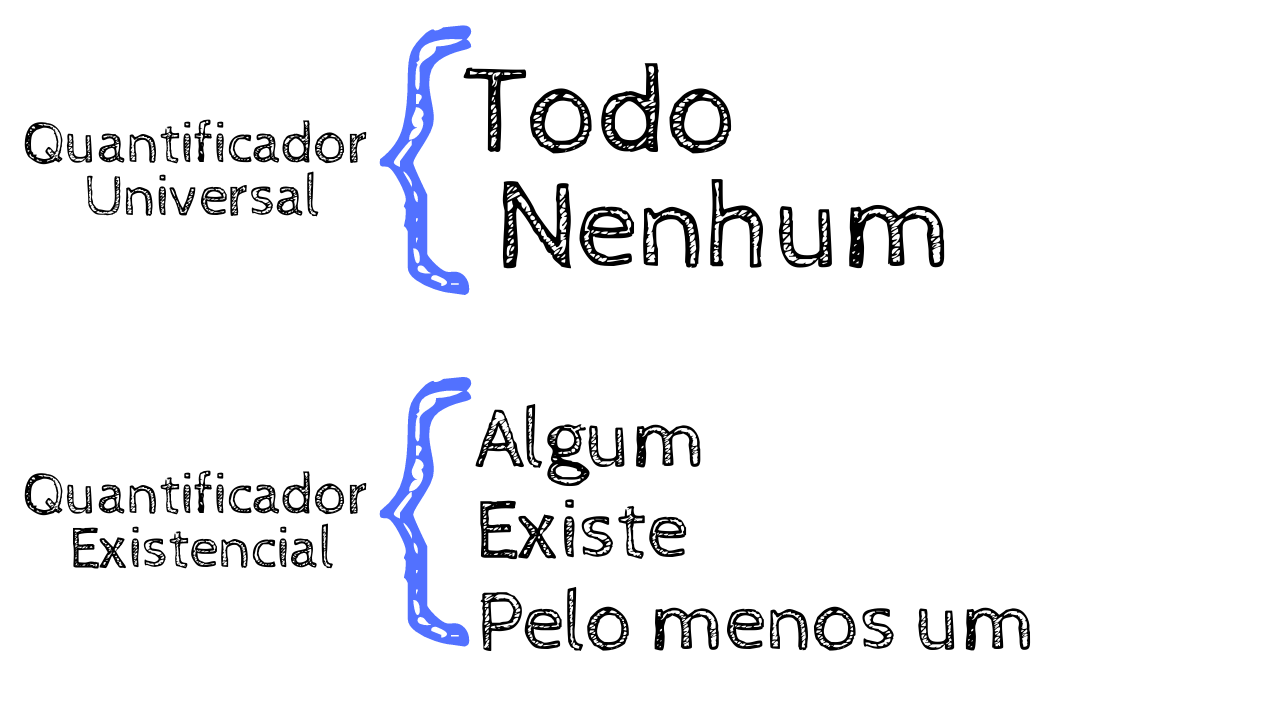
Além disso, as proposições podem ser afirmativas ou negativas.

Vamos aos exemplos.

CLASSIFICAÇÃO DAS PROPOSIÇÕES	EXEMPLOS
Proposição Universal Afirmativa	Todo doente é curável.
Proposição Universal Negativa	Nenhuma doença é curável.
Proposição Universal Negativa	Toda doença não é curável.
Proposição Existencial Afirmativa	Alguma doença é curável.
Proposição Existencial Afirmativa	Existe doença que é curável.
Proposição Existencial Afirmativa	Pelo menos uma doença é curável.
Proposição Existencial Afirmativa	Existe alguma doença que é curável.
Proposição Existencial Negativa	Alguma doença não é curável.
Proposição Existencial Negativa	Existe doença que não é curável.
Proposição Existencial Negativa	Pelo menos uma doença não é curável.
Proposição Existencial Negativa	Existe alguma doença que não é curável.

Há uma observação a ser feita aqui: a proposição universal negativa “Nenhuma doença é curável” é equivalente a dizer que “Toda doença não é curável”. Por consequência a expressão “nenhum” pode ser substituída pela expressão “Todo…não…”, ou seja, são proposições equivalentes.

Vamos ao ponto chave do nosso artigo. Queremos negar proposições quantificadas. Para tanto, seguiremos as seguintes regras:

– Caso o quantificador seja existencial, a negação usará um quantificador universal.

– Caso o quantificador seja universal, a negação usará um quantificador existencial.

– Se o verbo for afirmativo, a negação usará um verbo negativo.

– Se o verbo for negativo, a negação usará um verbo afirmativo.

Para facilitar ainda mais seu entendimento, colocaremos aqui alguns exemplos.

Exemplo 1

P: Nenhum carioca é corintiano.

P: Todo carioca é corintiano.

Conforme já mencionamos, as duas proposições acima são equivalentes e, consequentemente, possuem a mesma classificação: proposição universal negativa.

Pelas regras mencionadas, sua negação será uma proposição existencial afirmativa.

~p: Algum carioca é corintiano.

~p: Existe carioca que é corintiano.

~p: Existe algum carioca que é corintiano.

~p: Pelo menos um carioca é corintiano.

As quatro proposições acima são equivalentes.

Exemplo 2

p: Algum brasileiro é patriota.

p: Existe brasileiro patriota.

As duas proposições acima são equivalentes e, consequentemente, possuem a mesma classificação: proposição existencial afirmativa.

Pelas regras mencionadas, sua negação será uma proposição universal negativa.

~p: Nenhum brasileiro é patriota.

~p: Todo brasileiro é patriota.

Exemplo 3

p: Toda meditação é relaxante.

A proposição acima é uma proposição universal afirmativa.

Pelas regras mencionadas, sua negação será uma proposição existencial negativa.

~p: Alguma meditação não é relaxante.

~p: Existe meditação que não é relaxante.

~p: Existe alguma meditação que não é relaxante.

~p: Pelo menos uma meditação não é relaxante.

Exemplo 4

p: Algum estudante não é motivado.

p: Existe estudante que não é motivado.

Conforme já mencionamos, as duas proposições acima são equivalentes e, consequentemente, possuem a mesma classificação: proposição existencial negativa.

Pelas regras mencionadas, sua negação será uma proposição universal afirmativa.

~p: Todo estudante é motivado.

Nesses quatro exemplos trouxemos todas as situações possíveis de modo que a assimilação das situações propostas te levará ao sucesso na resolução das questões de concursos envolvendo a negação dos quantificadores todo, algum e nenhum.

Agora vamos colocar em prática todo conhecimento adquirido.

Estamos disponibilizando na sequência um Quiz cujo objetivo principal é fazer você fixar e amadurecer ainda mais seus conhecimentos em negação dos quantificadores todo, algum e nenhum.

Espero que você tenha obtido bons resultados nesse Quiz, mas não se apavore caso não tenha obtido bons resultados.

O importante agora é rever o que você errou e reforçar o que você acertou.

Dessa forma, vamos fazer a resolução das quatro questões propostas no Quiz.

Resolução do Quiz

1 – Considere a seguinte afirmação:

Todo homem é trabalhador.

A alternativa que apresenta uma negação lógica para essa afirmação é:

• Nenhum homem é trabalhador.
• Toda mulher é trabalhadora.
• Não existe homem que não é trabalhador.
• Todo trabalhador não é homem.
• Existe homem que não é trabalhador.

Resolução

O enunciado apresenta a seguinte afirmação: “Todo homem é trabalhador”.

Vamos iniciar fazendo a classificação dessa proposição.

A proposição é classificada como proposição universal afirmativa. O enunciado pede a negação lógica dessa proposição.

Sua negação será uma proposição existencial negativa.

Pelo que estudamos e pela classificação da sua negação, temos quatro opções de respostas:

– Algum homem não é trabalhador.

– Existe homem que não é trabalhador.

– Pelo menos um homem não é trabalhador.

– Existe algum homem que não é trabalhador.

Colocamos todas as opções aqui para facilitar o seu entendimento e para ampliar as suas possibilidades de resposta.

Pelas alternativas listadas na questão, podemos afirmar que a quinta alternativa apresenta a resposta correta.

2 – Considere a seguinte proposição:

 “Todos os profissionais formados pela Faculdade Alfa estão empregados”.

Admitindo que ela seja falsa, então certamente

• Todos profissionais formados pela Faculdade Alfa estão desempregados.
• Existe pelo menos um profissional formado pela Faculdade Alfa que não está empregado.
• Se o profissional Roberto está desempregado, então ele é formado pela Faculdade Alfa.
• Nenhum profissional formado pela Faculdade Alfa está empregado.
• Alguns profissionais formados pela Faculdade Alfa estão empregados.

Resolução

O enunciado indica que a seguinte proposição é falsa: “Todos os profissionais formados pela Faculdade Alfa estão empregados”.

Em seguida, temos que indicar qual das alternativas traz a proposição cujo valor lógico é verdade.

Temos que fazer a negação da proposição que contém o quantificador “Todos”.

Vamos iniciar fazendo a classificação. A proposição é classificada como proposição universal afirmativa.

A sua negação é uma proposição existencial negativa.

Vamos listar algumas das possíveis respostas:

– Alguns profissionais formados pela Faculdade Alfa não estão empregados.

– Existem profissionais formados pela Faculdade Alfa que não estão empregados.

– Pelo menos uns profissionais formados pela Faculdade Alfa não estão empregados.

– Existem alguns profissionais formados pela Faculdade Alfa que não estão empregados.

A partir dessas possíveis respostas, podemos afirmar que a segunda alternativa contém a resposta correta.

3 – Qual das seguintes alternativas apresenta a contraditória da afirmação: “Todo condenado é culpado.”?

•  “Todo condenado não é culpado.”.
• “Algum culpado é condenado.”
• “Algum condenado não é culpado.”
• “Algum condenado é culpado.”
• “Todo culpado é condenado.”

Resolução

Queremos aqui o contraditório da afirmação “Todo condenado é culpado”.

Em relação ao significado, a palavra “contraditória” indica que há divergência, ou seja, no sentido de contrário, inverso ou aposto.

Trazendo para o nosso contexto, queremos encontrar a negação da afirmação apresentada no anunciado.

A proposição “Todo condenado é culpado” é classificada como proposição universal afirmativa.

A sua negação é uma proposição existencial negativa.

Vamos listar algumas das possíveis respostas:

– Algum condenado não é culpado.

– Existe condenado que não é culpado.

– Pelo menos um condenado não é culpado.

– Existe algum condenado que não é culpado.

A partir dessas possíveis respostas, podemos afirmar que a terceira alternativa contém a resposta correta.

4 – Considere a afirmação:

“Existem insetos que não são pretos”

Se essa afirmação é falsa, então é verdade que

• nenhum inseto é preto.
• todo inseto é preto.
• todos os animais pretos são insetos.
• nenhum animal preto é inseto.
• nem todos os insetos são pretos.

Resolução

A proposição “Existem insetos que não são pretos” é classificada como proposição existencial negativa.

A sua negação é classificada como proposição universal positiva.

Para essa classificação temos a seguinte resposta: “Todos os insetos são pretos” ou no singular “Todo inseto é preto”.

Podemos afirmar que a segunda alternativa apresenta a resposta correta.

Muito bem! Finalizamos a nossa resolução. Espero que os exercícios propostos tenham ajudado na fixação e entendimento do conteúdo proposto nesse artigo.

Para encerrarmos  com chave de ouro, disponibilizo para você um vídeo contendo a explicação do conteúdo e a resolução dos exercícios propostos no Quiz.

Espero que ao longo desse artigo você tenha sanado todas as suas dúvidas sobre negação dos quantificadores todo, algum e nenhum.

Se mesmo assim, você ainda estiver com dificuldades no entendimento desse conteúdo, deixe um comentário.

Responderemos o mais breve possível!